M3

Introduction

由于开始的时间比较晚，在老师的 wiki 上无法下载 gpt.c 的 model 文件，所以网上找。

Basic knowledge of AI

由于自己不像南大的学生可能在上 OS 课前就有 AI 相关的基础，所以这部分我根据老师推荐的学习资料和 LLM 来一步步学习相关概念，当然只是大概过一遍内容。

首先，gpt.c 的源代码就是最好的老师！它实现了对神经网络的 “真正数学严格” 的描述——如果我们看 PyTorch 的代码，其中会涉及许多内置的算子，你对其中的实现其实并不 100% 理解——但对于 C 代码这种语义 “扁平” 的语言来说，你真的可以完全理解它！此外，我们给一个外链，也还推荐 Understanding Deep Learning。

当然，老师上面给出的一些学习资料也很不错！

加上之前偶然刷到的视频：从函数到神经网络【白话DeepSeek01】和 Neural network (machine learning)，应该能简单了解。最后再看看神经网络中的相关概念是怎么对应 C 代码实现。

overview

一、神经元

神经元是神经网络的基本组成单元，它模拟了生物神经元的行为。一个简单的神经元模型由以下部分组成：

输入连接 ：接收来自其他神经元或输入数据的信号。
权重：每个输入连接都有一个权重，表示该输入对神经元输出的重要性。
偏置：一个常数，用于调整神经元的激活阈值。
激活函数 ：对神经元的加权输入进行非线性变换，以决定神经元是否被激活。

神经元的输出 y 的数学表达式： $$ y = \sigma\left( \sum_{i=1}^{n} w_i x_i + b \right) \

x_i 是输入，w_i 是权重，b 是偏置，\sigma 是激活函数 $$

二、激活函数

激活函数是神经元中用于引入非线性的关键组件，它使得神经网络能够学习复杂的模式和特征。常见的激活函数有：

Sigmoid 函数
- 数学表达式 ： $$ \sigma(x) = \frac{1}{1 + e^{-x}} $$
- 特点：输出范围在 (0,1) 之间，可以将任意实数值映射到 0 和 1 之间，常用于二分类问题。然而，Sigmoid 函数在输入较大或较小时会出现梯度饱和问题，导致训练速度变慢。
- 应用场景 ：适用于二分类任务的输出层，也可用于某些需要将输出限制在 0 到 1 之间的中间层。
ReLU 函数（Rectified Linear Unit）
- 数学表达式 ： $$ \text{ReLU}(x) = \max(0, x) $$
- 特点：当输入大于 0 时，输出等于输入；当输入小于等于 0 时，输出为 0。计算简单，能有效缓解梯度消失问题，但在输入小于 0 时梯度为 0，可能导致部分神经元 “死亡”。
- 应用场景 ：广泛应用于卷积神经网络（CNN）和多层感知机（MLP）等的隐藏层。
tanh 函数
- 数学表达式 ： $$ \tanh(x) = \frac{e^{x} - e^{-x}}{e{x} + e^{-x}} $$
- 特点：输出范围在 (-1,1) 之间，是非线性函数，能够将输入数据归一化到 -1 到 1 的区间。相比 Sigmoid 函数，tanh 函数的输出均值更接近 0，有助于加快收敛速度，但也存在梯度饱和问题。
- 应用场景 ：常用于循环神经网络（RNN）和某些需要将输出限制在 -1 到 1 之间的场景。
GELU 函数（Gaussian Error Linear Unit）
- 数学表达式 ： $$ \text{GELU}(x) = x \cdot \Phi(x)，\ \Phi(x) 是标准正态分布的累积分布函数。 $$
- 特点：结合了 ReLU 和线性函数的优点，具有更好的非线性拟合能力，在 Transformer 模型中被广泛使用。
- 应用场景 ：适用于 Transformer 架构的神经网络，特别是在自然语言处理任务中。
Softmax 函数
- 数学表达式 ：
  
  对于输入向量： $$ z = [z_1, z_2, ..., z_n] $$ Softmax 函数的输出为： $$ \text{Softmax}(z_i) = \frac{e^{{z_i}}{\sum_{j=1}}{n} e^{z_j}} \ (i = 1, 2, ..., n) $$
- 特点：将一组实数值转换为概率分布，使得所有输出值的和为 1，常用于多分类问题的输出层。
- 应用场景 ：主要用于多分类任务的输出层，将神经网络的输出转换为各类别的概率。
Leaky ReLU 函数
- 数学表达式 ： $$ \text{Leaky ReLU}(x) = \begin{cases} x, & x > 0 \ \alpha x, & x \leq 0 \end{cases} \ \alpha 是一个较小的正数，如 0.01 $$
- 特点：在输入小于 0 时，输出为 αx ，避免了 ReLU 函数中部分神经元 “死亡” 的问题，同时保留了 ReLU 函数在输入大于 0 时的线性特性。
- 应用场景 ：适用于需要解决 ReLU 函数 “死亡” 问题的神经网络隐藏层。
ELU 函数（Exponential Linear Unit）
- 数学表达式： $$ \text{ELU}(x) = \begin{cases} x, & x > 0 \ \alpha (e^{x} - 1), & x \leq 0 \end{cases} \ \alpha 是一个正数 $$
- 特点：在输入小于 0 时，输出为 (\alpha (e^{x} - 1))，能够平滑地过渡到负值，有助于缓解梯度消失问题，同时避免了神经元 “死亡” 现象。
- 应用场景 ：适用于需要更好收敛性能和避免神经元 “死亡” 的神经网络隐藏层。

三、神经网络的结构

一个典型的神经网络由以下几层组成：

输入层

负责接收输入数据，其神经元数量通常与输入特征的维度一致。
隐藏层

位于输入层和输出层之间的层，可以有多个隐藏层，每个隐藏层包含一定数量的神经元。隐藏层通过非线性激活函数对输入数据进行特征提取和变换。
输出层

产生神经网络的最终输出结果，其神经元数量取决于任务的类型，例如在分类任务中，输出层神经元数量通常与类别数一致。

直接配图，当然实际情况更加复杂！

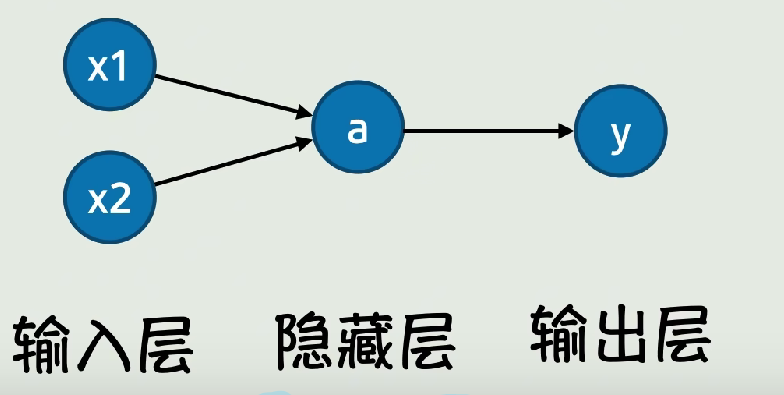
四、矩阵运算在神经网络中的应用

在神经网络中，矩阵运算是高效实现神经元计算的关键。

例如，对于一个包含多个神经元的层，我们可以将输入数据、权重和偏置表示为矩阵和向量，然后通过矩阵乘法和加法运算快速计算出该层所有神经元的输出。

假设输入数据为一个 (m \times n) 的矩阵 (X)（表示有 (m) 个样本，每个样本有 (n) 个特征），权重矩阵为一个 (n \times p) 的矩阵 (W)（表示从输入层到隐藏层的连接权重，隐藏层有 (p) 个神经元），偏置向量为一个 (1 \times p) 的向量 (b)，则隐藏层的输出矩阵 (H) 可以通过以下矩阵运算得到：

$$ H = \sigma(X \cdot W + b) \ \sigma 表示逐元素应用激活函数。 $$

五、层归一化（Layer Normalization）

层归一化是一种对神经网络中间层的输出进行归一化的技术，旨在稳定网络的训练过程和提高收敛速度。它通过对每个样本在每个神经元上的输出进行归一化，使得这些输出具有零均值和单位方差，然后通过学习的参数进行缩放和平移操作。

对于输入数据 (x)，层归一化的输出 y 数学表达计算如下： $$ y = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta \ \mu 和\sigma^2 分别是输入数据在该层神经元上的均值和方差 \ \gamma 和 \beta 是学习的缩放和平移参数 \ \epsilon 是为了避免除零的微小常数。 $$

六、注意力机制（Attention）

注意力机制是现代神经网络，特别是 Transformer 模型中的核心组件之一。它允许模型在处理序列数据时，能够动态地关注序列中的不同位置，从而更好地捕捉序列中的长期依赖关系。

自注意力（Self-Attention）

自注意力机制通过计算序列中每个位置的查询向量（Query）、键向量（Key）和值向量（Value）之间的相似度，来确定每个位置应该关注的其他位置的程度。具体步骤如下：

生成 Q、K、V 向量 ：对输入序列中的每个元素，通过线性变换生成查询向量 (Q)、键向量 (K) 和值向量 (V)。
计算注意力分数 ：通过 (Q) 和 (K) 的点积计算注意力分数，表示每个位置之间的相关性。
缩放和 softmax 操作 ：将注意力分数除以键向量维度的平方根进行缩放，然后应用 softmax 函数得到注意力权重，这些权重表示每个位置应该分配多少关注给其他位置。
加权求和 ：将注意力权重与对应的值向量进行加权求和，得到最终的输出。

七、软件最大值函数（`Softmax`）

Softmax 函数常用于神经网络的输出层，特别是在多分类问题中。它将一组实数值转换为概率分布，使得所有输出值的和为 1。

对于输入向量 $$ z = [z_1, z_2, ..., z_n] $$ Softmax 函数的输出为： $$ \text{Softmax}(z_i) = \frac{e^{{z_i}}{\sum_{j=1}}{n} e^{z_j}}\

(i = 1, 2, ..., n) $$

八、残差连接（Residual Connection）

残差连接是一种网络结构设计，它通过将输入直接加到输出上，形成一个残差块。这种设计有助于缓解深度神经网络中的梯度消失问题，使得网络能够更容易地训练更深的层次。

残差块的输出 (y) 的数学表达：

$$ y = F(x) + x\ x 是输入，F(x) 是残差块中的主路径网络结构的输出。 $$

九、Transformer 模型概述

Transformer 模型是一种基于自注意力机制的神经网络架构，广泛应用于自然语言处理任务中，如机器翻译、文本生成等。它主要由以下组件构成：

编码器（Encoder） ：对输入序列进行编码，提取特征表示。
解码器（Decoder） ：根据编码器的输出和之前的解码结果生成输出序列。
自注意力层（Self-Attention Layer） ：在编码器和解码器中都使用，用于捕捉序列中的依赖关系。
前馈神经网络（Feed-Forward Neural Network） ：对每个位置的特征进行非线性变换。

十、GPT-2 模型简介

GPT-2 是一种基于 Transformer 架构的预训练语言模型，它通过在大规模文本数据上进行无监督预训练，学习到了丰富的语言知识和语义信息。GPT-2 主要由多个 Transformer 解码器层堆叠而成，每个解码器层包含自注意力机制和前馈神经网络。在实际应用中，可以通过微调 GPT-2 模型来适应特定的自然语言处理任务，如文本生成、问答系统等。

Usage of Tools

主要是 perf。先借助 LLM 给出使用总结：

以下是perf的基本使用方法总结：

基础用法

安装perf：大多数Linux发行版都自带perf工具，通常作为perf包提供。如果没有安装，可以通过包管理器安装，例如在Ubuntu上可以使用sudo apt-get install linux-tools-generic命令。

启动perf记录：使用perf record命令来记录程序的性能数据。例如，perf record ./your_program会记录your_program运行时的性能事件。

停止perf记录：在记录过程中，可以按Ctrl+C组合键来停止记录。

查看perf报告：使用perf report命令来查看记录的性能数据报告。

常见使用场景

性能分析：使用perf top命令可以实时查看系统中各个进程的性能事件统计，类似于top命令。

事件监测：perf可以监测多种性能事件，如CPU周期、缓存引用、分支指令等。可以通过perf stat命令来获取这些事件的统计信息。

系统资源监控：使用perf record -e sched:sched_switch -a可以记录系统中进程调度切换的事件，帮助分析系统资源的使用情况。

示例
记录并分析程序性能：
perf record ./your_program
perf report
实时查看性能事件统计：
perf top
监测特定性能事件：
perf stat -e cycles,instructions ./your_program

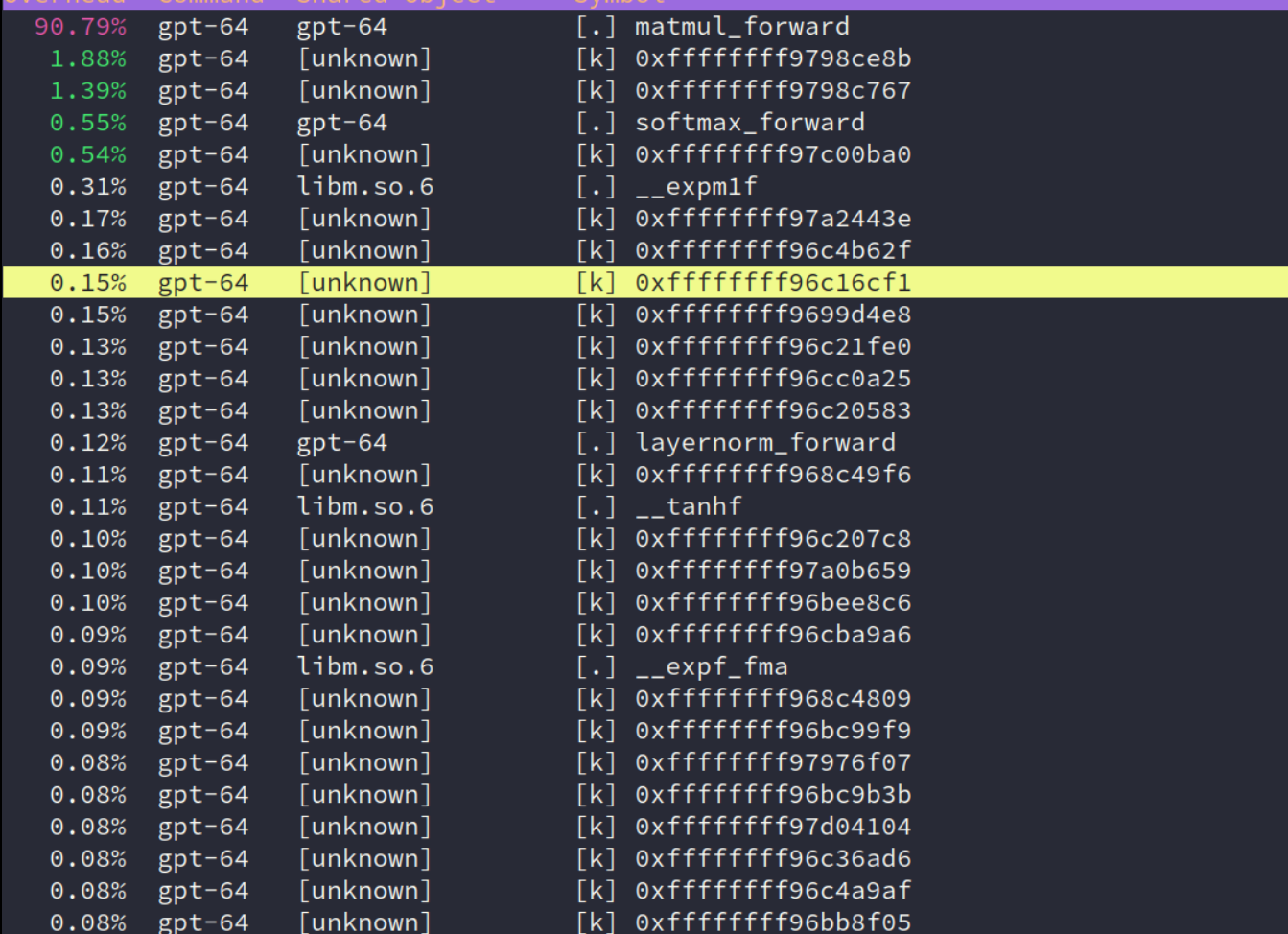
由此得出我的性能瓶颈：

lab

好的！既然你希望从零开始理解神经网络的基础知识，并通过分析 gpt.c 的源码来学习，我会用 分层递进 的方式，结合代码实例和核心概念，帮助你建立完整的知识框架。以下是学习路径：

第一阶段：神经网络基础概念

1. 神经元与激活函数

神经元：模拟生物神经元，接收输入信号，加权求和后通过激活函数输出。
激活函数：决定神经元是否被激活（如 ReLU, Sigmoid, GELU）。

代码示例：gpt.c 中的 gelu_forward 函数：

void gelu_forward(float* out, float* inp, int N) {
    for (int i = 0; i < N; i++) {
        float x = inp[i];
        float cube = 0.044715f * x * x * x;
        out[i] = 0.5f * x * (1.0f + tanhf(GELU_SCALING_FACTOR * (x + cube)));
    }
}

作用：对输入 inp 的每个元素应用 GELU 激活函数，结果存入 out。

2. 矩阵运算（Matrix Operations）

权重矩阵：神经网络的参数，用于线性变换。
矩阵乘法：神经网络的核心计算（如全连接层）。

代码示例：matmul_forward 函数：

// 输入 inp (B,T,C), 权重 weight (OC,C), 输出 out (B,T,OC)
for (int o = 0; o < OC; o++) {
    float val = bias[o]; 
    for (int i = 0; i < C; i++) {
        val += inp_bt[i] * weight[o*C + i];  // 点积运算
    }
    out_bt[o] = val;
}

作用：将输入向量与权重矩阵相乘，得到输出。

3. 前向传播（Forward Propagation）

过程：输入数据从输入层逐层计算到输出层。
代码体现：gpt2_forward 函数中的逐层调用（如 encoder_forward, layernorm_forward）。

第二阶段：理解 `gpt.c` 的代码结构

1. 模型参数（ParameterTensors）

存储权重：如 wte（词嵌入矩阵）、wpe（位置编码矩阵）。

代码结构：

typedef struct {
    float* wte;  // (V, C)
    float* wpe;  // (maxT, C)
    float* ln1w; // LayerNorm 的权重
    // ... 其他参数
} ParameterTensors;

2. 激活与中间结果（ActivationTensors）

存储中间值：如 encoded（编码后的输入）、att（注意力分数）。

typedef struct {
    float* encoded; // (B, T, C)
    float* ln1;     // LayerNorm 后的结果
    // ... 其他激活
} ActivationTensors;

3. 核心函数解析

编码层：encoder_forward
输入：Token ID → 查表得到词嵌入（wte）和位置编码（wpe）。

代码逻辑：

// 将 token 和位置编码相加
for (int i = 0; i < C; i++) {
    out_bt[i] = wte_ix[i] + wpe_t[i];
}

注意力机制：attention_forward
步骤：计算 Query、Key、Value → 计算注意力分数 → Softmax → 加权求和。

代码关键点：

// 计算 Query 和 Key 的点积
for (int i = 0; i < hs; i++) {
    val += query_t[i] * key_t2[i];
}

第三阶段：从代码看神经网络细节

1. 层归一化（LayerNorm）

作用：对每个样本的特征进行归一化，加速训练。

代码实现：layernorm_forward 函数：

// 计算均值和方差
for (int i = 0; i < C; i++) {
    m += x[i];
}
m = m / C;
// 归一化并缩放
for (int i = 0; i < C; i++) {
    float n = (s * (x[i] - m));
    out_bt[i] = n * weight[i] + bias[i];
}

2. 残差连接（Residual Connection）

作用：缓解梯度消失，允许深层网络训练。

代码体现：residual_forward 函数：

for (int i = 0; i < N; i++) {
    out[i] = inp1[i] + inp2[i];  // 输入 + 输出
}

第四阶段：并行化思路分析

1. 找到计算热点

时间分析：使用 Profiler（如 perf）发现 matmul_forward 和 attention_forward 是性能瓶颈。

2. 矩阵乘法的并行化

策略：将输出通道（OC）分块，每个线程处理一部分。

代码修改：

// 原始代码（串行）
for (int o = 0; o < OC; o++) {
    // 计算每个输出通道
}

// 并行化：每个线程处理 OC/NUM_THREADS 个通道
void matmul_worker(int o_start, int o_end) {
    for (int o = o_start; o < o_end; o++) {
        // 计算部分通道
    }
}

3. 注意力机制的并行化

策略：将注意力头（NH）分给不同线程。